Comparing Predictions with Relative Brier Score
Manifold user "wasabipesto" has created "brier.fyi": a new website that compares the performance of online prediction markets and forecasting sites. The site currently tracks markets from Kalshi, Manifold, Metaculus, and Polymarket. It's quite well-done, and provides a number of different charts and statistics with friendly letter-grade summaries.
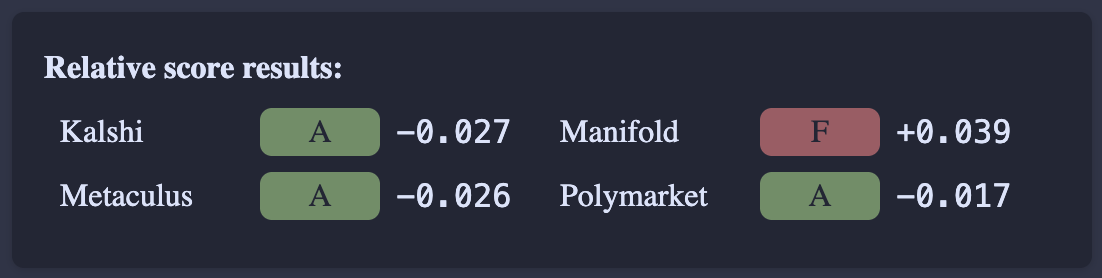
I'd say the key piece of analysis is a direct comparison where a number of markets that existed on multiple platforms were used to compare the platforms against each other:
Making all these tools to label these markets and analyze them seems like a lot of work, so kudos to wasabipesto for doing this!
Manifold is doing pretty badly
As you can see, Manifold is doing pretty badly compared to the other markets. Some people on the Manifold Discord proposed a few reasons this might be the case, like:
Manifold has more markets in total, so each individual market will have fewer traders, and less attention, and will therefore be less accurate.
Manifold's markets are user created and are therefore more likely to be less well-defined than the comparable markets on the other platforms. This creates more noise around the resolution criteria which makes the Manifold markets harder to predict.
I was still pretty surprised to see that things were this bad, so I wanted to look into what seemed to be different about Manifold in the data for specific questions. One thing I quickly noticed was that Manifold was often one of the first platforms to start predicting a question (which makes sense given the high volume of markets it creates).
This made me wonder: How does the site compare markets that make predictions over different time ranges? This seemed like a question without an obvious answer, and a potential source of bias in the results.
The Relative Brier score
Here's the description from the site for how it does the comparison. Note that this methodology actually comes from Cultivate labs. I'll transcribe the brier.fyi description:
Our first step is preprocessing - for every market we average the probability over each day to minimize transient spikes and normalize the data.
Next we narrow the range down to the period where at least two markets are open. For some markets we will also override the start or end dates to limit the scoring period.
For each day in the scoring range, we calculate the score for each market. In this case we will use the Brier score, but other scores such as log would also work. This is the daily absolute score.
We then calculate the median daily score as a baseline for comparison. Markets that do better than this median will have better scores at the end.
For each day, we find the difference between each market's daily absolute score and that median.
Finally, we sum all of the market's daily differences and divide them by the total number of scoring days. Not all markets are open for the same duration, so this grants better scores to the markets that were open for longer.
This raised a few red flags for me:
The "this grants better scores to the markets that were open for longer" part
Why is this fair? If a particular market isn't open for a long time, it might just be a choice on the part of the platform creators to only forecast once they felt comfortable they could make a valuable prediction. Shouldn't that be something we want to incentivize?
Why is this even true? In fact, it seems like whatever set of scores result in an advantage to longer markets, we could just take the opposite of those score to get a situation that disadvantages longer markets.
It seemed weird to use the median, given that this was a quantity we were averaging over time. I think it's usually more common to use the mean for this kind of thing to be able to reason about the system using linearity of expectation.
Why using the median is weird and doesn't necessarily advantage long-term predictions
One can view the relative Brier score as a way of imputing missing data from predictors who aren't present in a particular market at a particular time. Specifically, the relative Brier score assumes that such a predictor would have received the median score.
Is this reasonable to assume? In some cases one can argue that it is. For example if there are an odd number of predictors then the predictor who receives the median score is just the predictor who assigns the median probability. Thus, if you assume that the absent predictor would have just looked at the field and used the median prediction, then the imputed score lines up.
But on the other hand, if there are an even number of predictors, then the median score is the average of the scores of the middle two predictions. Is this score by predicting the average of the predictions of the two middle predictors? No.! Because the Brier score is convex, the score of the median of the predictions, will actually paradoxically be better than the median score! This puts a damper on the interpretation that we are imputing an aggregate prediction onto the missing data.
Another way to look at this is in terms of the average as an alternative. If we expect predictors to want to maximize their average score relative to the other predictors, then it makes sense to ask "does making more predictions at earlier times tend to help or hurt the average?". When there are only four predictors we can break this down into four cases:
When there is only one predictor, there is no one to compare to and this data isn't included in the average relative score.
When there are exactly two predictors, the median score is just the average score of the two predictors. Thus, the average score when two predictors are present is always zero, and so the net score accumulated at these times is zero.
When there are exactly three predictors, the fourth missing predictor is imputed to have the prediction of the middle predictor. Thus, whether the net score accumulated at such times is positive or negative depends on whether the median is greater than the mean.
When there are exactly four predictors, there is no imputed data. Thus, the net relative score is again zero because all four scores are being compared to their average.
So we are left with the strange situation where it is possible for the total relative Brier score to be nonzero. But the only times at which a non-zero score can accumulate are times at which exactly three predictors are present. Looking at the image above, the scores indeed sum to a negative number, meaning that it is better to predict more when there are exactly three predictors present.
Going Meta: Why predict rather than aggregate?
Happily, the creator of the brier.fyi site came back with a re-analysis of the data using the mean rather than the median, showing that there was not much of a high-level difference. Again, many thanks! But let me nevertheless conclude with some high-level criticism in the spirit of the Prediction Market FAQ that I feel this experience has left me with.
I asked whether it was reasonable to assume an absent predictor would have achieved the relative Brier score in the counterfactual where they did predict. Perhaps a better question is: Why didn't the predictors who did predict all achieve this score? After all, I showed that making the median prediction always gets a score as good as or better than the median score. These predictions are all public, so in principle, traders on these markets who did this aggregation could have moved the predictions of the markets in this direction.
A similar criticism goes for computing the calibration of markets, which is another metric that brier.fyi computes. It is great to see the calibrations of these markets, but in principle any market that has a trader betting on the principle that markets at a certain price level are consistently overpriced or underpriced should fix the calibration in the long term.
In the future, I hope people ask fewer questions like:
Which market performed better?
Which market is better calibrated?
And more questions like:
What are the points of financial friction to trading on a particular market?
What makes it hard to profitably arbitrage some prediction markets against others?
How profitable would a particular simple strategy or investment thesis have been on a particular market over a long time frame?