Quantum Bitcoin Mining
This post assumes some basic knowledge of Proof-of-Work/"Nakamoto" consensus
I have long been dissatisfied by the state of public discourse about the consequences of quantum computing for blockchains. In particular, I find that most popular articles focus only on the threat posed by Shor’s algorithm. Very few mention Grover's algorithm, and when they do, they often incorrectly claim that it’s not an issue since it “doesn’t provide an exponential speedup”.
This culminated for me in an interview a few months ago of quantum computing luminary Scott Aaronson by the blockchain podcast “Bankless”. The tagline of Aaronson's blog is "quantum computers won't solve hard problems instantly by just trying all solutions in parallel". Surely this is someone who can elucidate the subtle issues behind this concept.
Unfortunately, while Aaronson does better than everyone else, he still gets a key point wrong. He says (at around the 1:18:32 mark):
... if you got to a world where just about everyone had access to a quantum computer then it’s kind of amusing what would happen, which is that the proof of work just has its hardness just set automatically based on how much mining people have been able to do recently, and so all that would happen would be that pre-images would have to satisfy an ever more stringent condition, and the proof of work would automatically just be made harder to compensate for Grover’s algorithm, and we would all just be back where we started
This is a misconception, and it’s unfortunate because the consequences of Grover's algorithm for mining are actually quite interesting, both as an object of academic study, and in terms of their consequences for the long-term viability of proof of work. I'm making this post to set the record straight by explaining why all of these claims are wrong, and to explore some consequences of Grover's algorithm for mining through the lens of a few papers (one of which I co-wrote).
Overview of Grover's Algorithm in Simple Terms
The other main impetus for me writing this blog post now is the recent YouTube video explaining Grover’s algorithm from the high-profile math explainer channel “3Blue1Brown”. Kudos to Grant Sanderson for making this! I encourage readers to watch the video, but if you really like my writing, I’ll put my own explanation in this section. Mine is a very high-level overview, and I'm not going to go into the matrix algebra or the quantum gates that are used to implement it - I think that focusing on that stuff scares off a lot of classical computer scientists who could otherwise understand and study the consequences of the algorithm perfectly well.
Grover's algorithm1 is an "unstructured search algorithm". This means it's useful for finding answers to what you might think of as "NP" problems. You provide Grover's algorithm with a description of a procedure for checking if a solution to your problem is correct. In the context of proof-of-work mining, the problem we are answering is "does a particular nonce lead to a valid bitcoin block".
Grover's algorithm provides two affordances that you can use to get your potential solution to your problem:
Applying a "Grover Iteration". This is a "turning the crank" operation2 that changes the internal structure of your quantum state. Note well that this process doesn't provide any information on its own. Its only usefulness is that it makes progress relevant to the second affordance...
Opening the register. This has a chance of giving you a solution to the problem. The probability of a success depends on the number k of Grover iterations applied, according to the formula
\(\approx \sin^2\left(\frac{2k+1}{\sqrt{N}}\right)\)where the fraction of possible solutions that turn out to actually be solutions is 1/N. This action also destroys/resets the register, leaving it as if zero iterations had been applied.
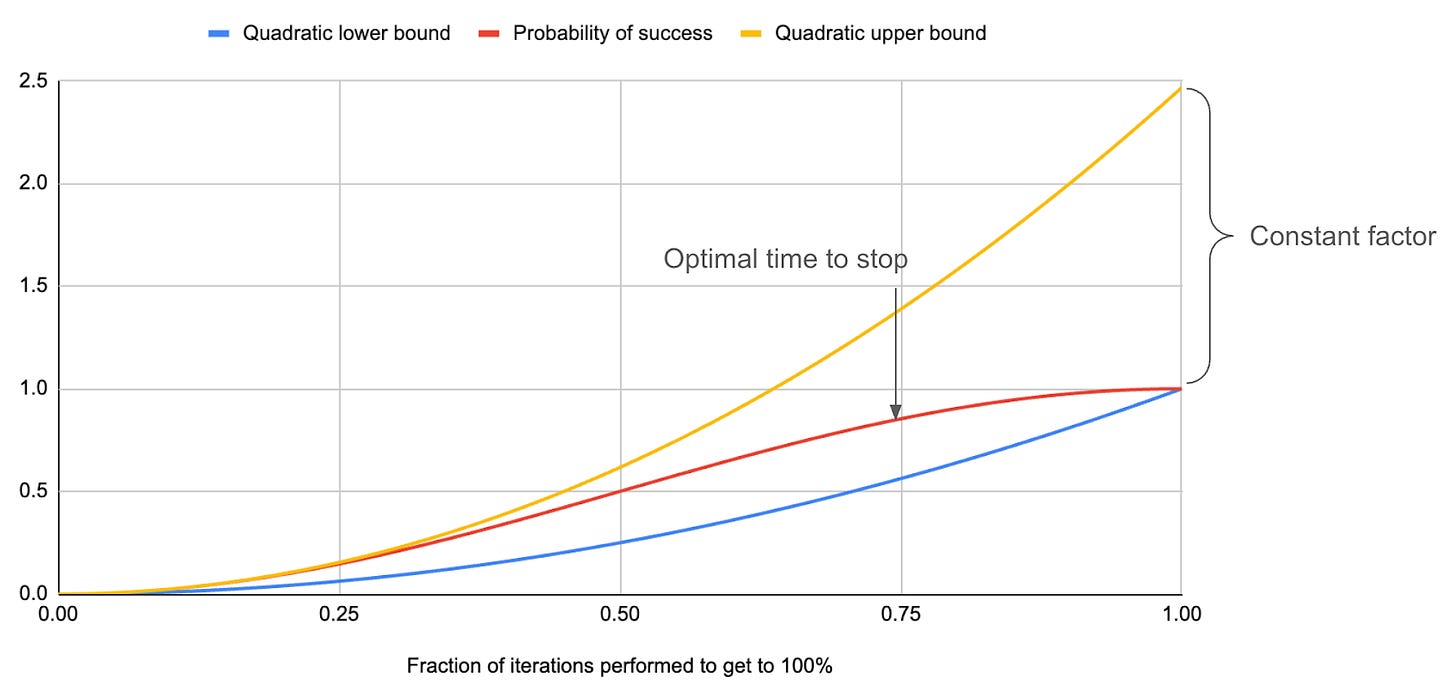
The key feature of these affordances is that the probability of success with Grover's algorithm goes up (within a constant factor of) quadratically with the number of iterations.
By applying k = 0.785 · √N iterations, we get a probability around 1 of successfully solving the problem3, but if we only carry out 1/100 as many iterations, our chance of solving the problem will be on the order of 1/10,000. The quadratic fits particularly nicely in the range of the initial few iterations, where all the higher-order terms of the power expansion of sin2 drop out.
Conditions for Advantageous Quantum Bitcoin Mining
For context, the current (May 2025) number of hashes needed to mine a Bitcoin block is N = 6 x 1023 . So if we had a quantum computer which could run Grover iterations at the same rate that a classical computer ran hashes, we would expect the quantum computer to mine a block almost a trillion times faster!
But this view oversells the quantum advantage. A key consideration is that even if a quantum computer mines an individual block a trillion times faster than an individual ASIC or ASIC core, the Bitcoin network as a whole will be much more powerful than that ASIC, and so it might still take hours or weeks or years for the quantum computer to finish mining. If so, it will be useless to Grover mine the block to 100% probability of success because by the time we are done, our block will certainly be stale.
The practical thing to do, therefore, is to stop the Grover process early so we can take advantage of what iterations we can complete before it's too late. But this opens up a host of other questions, about the best way of doing this. Luckily, there is a nice paper by Nerem and Gaur that provides some answers, which I will now relay:
How long should I compute Grover iterations before opening?
16 minutes.
Or, in general, about 1.593624 times the average block time of the blockchain in question. Surprisingly, this does not depend at all on the clock speed of the quantum computer in question!
How fast/cheap does quantum computing need to be to make it more profitable than normal mining?
This also depends on the block time, and is described by the formula
The answer is, in natural language, that the quantum computer is cheaper only if the ratio of the cost4 of a single Grover iteration to the cost of a classical hash is at most 2.59 times the number of iterations the miner can complete in one block time. Using some back-of-the-envelope math, the authors estimate the latter quantity at around 34,900 -- assuming a Quantum computer that operates at gate speeds of today’s quantum computers, but without the need for error correction5.
On the insecurity of quantum Bitcoin mining
Nothing in the “Conditions” paper above contradicts Aaronson’s “we would all just be back where we started” statement per se. But this is because that paper leaves out consideration of what happens if another block should come out while an aggressively-profit-maximising quantum miner is still in the middle of Grover iterating. As it turns out - the implications are massive for security. I'll switch now to covering an earlier paper by my colleague Or Sattath that treats this.
Consequences of opening blocks in response to new blocks
When a new longest-chain Bitcoin block is released, a classical miner is incentivized to stop working on their previous block and start working on the new one, because any blocks built on top of the new chain tip will themselves then be part of the longest chain, and will be likelier to be eventually confirmed. But with Grover, the functionality of the "opening" facility complicates things. If a miner is to stop working on their Grover block due to a new block coming over the network, they will lose all work done on that block to that point. Therefore, they might as well open the register they have immediately. The probability of success will be less than if they had mined for the full 16 minutes, but not negligible - if the block comes out 8 minutes into the mining period, for example (as more than 50% of blocks do6), the likelihood of success will be 1/4 what it would be after the full 16.
Calculating more precisely, if the probability of success of the quantum miner after 16 minutes is p, then the chances of various outcomes are as follows:
Modeling inter-block times with an exponential distribution, there is a 20.319% chance that the rest of the network fails to mine a block after 15.936 minutes.
If so, then there is a p probability that the quantum miner then succeeds, for a total chance of p · 0.20319 that the miner will mine a block without the classical network producing one.
There is a 79.681% chance that the rest of the network succeeds in mining a block.
In this case, the distribution over times the block could have been mined is a truncated exponential. We can integrate the success probability over this to get a p · 0.2125 chance of success in this conditional, or a p · 0.1693 total chance of successfully mining a block after a classical one is released.
So we get that a full 0.1693 / (0.1693 + 0.20319) = 45.45% of all blocks successfully mined by the quantum miner will come in response to other “sibling” blocks from the network mined at the same block height.
Impact on decentralization
In stark contrast to a classical miner, the vast majority of whose blocks won’t be siblings, a quantum miner can potentially almost double their income if they cause their aggressively-mined sibling blocks to be accepted7. This massively incentivizes them to seek out ways of making this happen. There are a number of ways they might do this:
They could make deals with other quantum miners, if they exist8, to respect each other blocks above others at the same height.
They could bribe classical miners or mining pools to accept their blocks.
This might not even require explicit collusion - the bribe could take the form of a UTXO in the blocks which can be spent by anyone, making petty-compliant9 miners prefer these blocks.
They can invest in acquiring a greater share of the total network hashrate than they otherwise would, since all the hashrate they acquire gives them the same benefits it would give to another miner, but with the added bonus of the selfish mining.
Incentives for this kind of collusion bring the fundamental assumptions of the fairness and decentralization of Bitcoin mining into question. If we live in a world where miners are incentivized to make deals and join forces, then it becomes likely that we will eventually reach a position where a single entity has a majority of the hashpower, and therefore unilateral authority over which blocks are included in the chain. A key point is that while it's possible to have a stale block in classical Bitcoin mining due to network delay, these are very infrequent, and their rarity removes a lot of the incentive to collude.
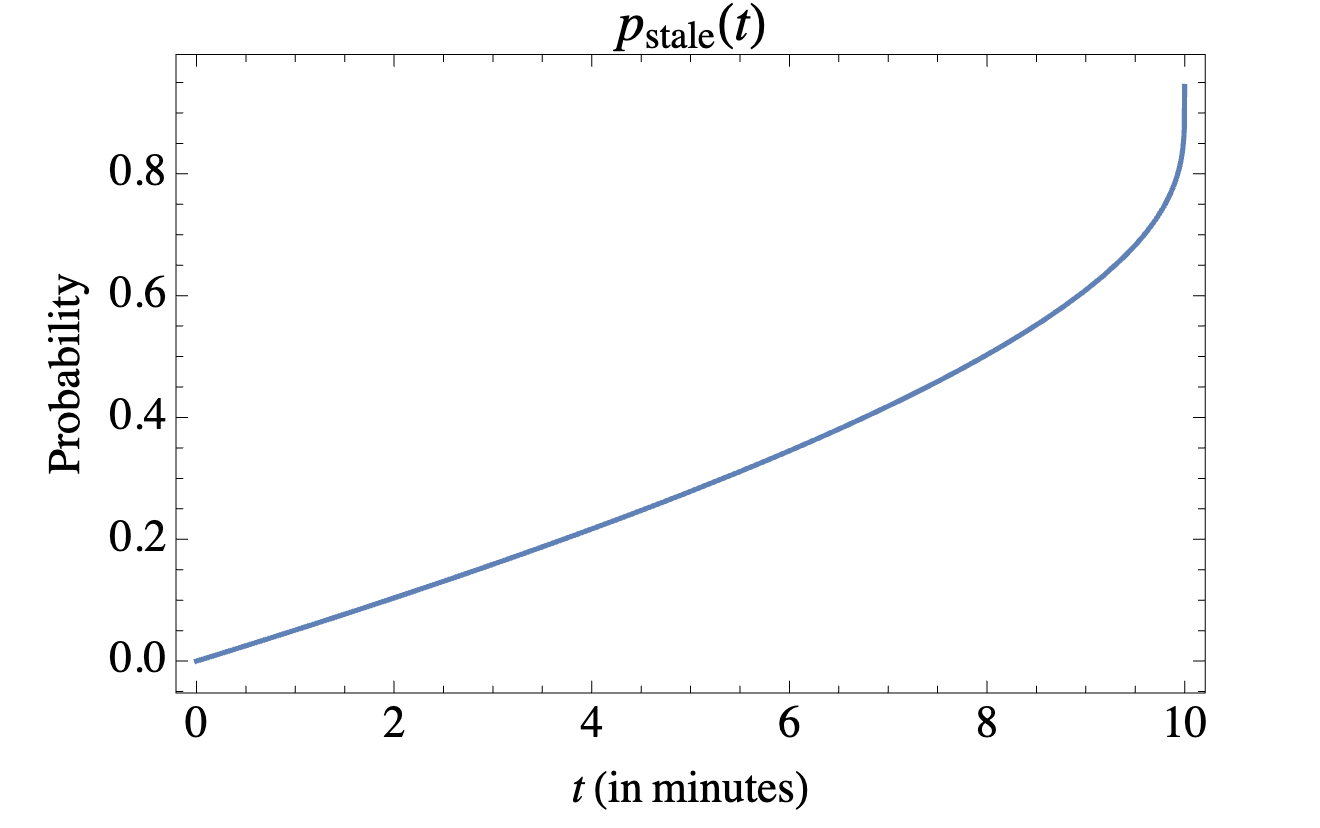
How much higher is the stale rate in a world of only quantum miners?
Or's paper calculates the stale rate, the ratio of blocks released after an already mined block on the same height, under the assumption that all miners are quantum and plan to measure after a fixed time t. The formula is
Where t is in units of block times.
Here is a figure from the paper:
Suffice it to say, depending on the dynamics of the miners’ measuring times, this can turn out even worse than the case where most miners are classical.
Quantum Time-Warp Attacks
Finally, I’ll discuss a paper “51% Attack via Difficulty Increase with a Small Quantum Miner” that I wrote with Or covering how quantum attacks that manipulate timestamps can actually be used to completely attack a proof-of-work chain using the difficulty adjustment mechanism. Timestamp manipulation attacks are sometimes called “Time-Warp attacks”, but I was a bit concerned that if we titled the paper “Quantum Time-Warp Attacks” any reviewer who looked at the paper would think we were cranks.
Bitcoin’s Difficulty Adjustment Mechanism
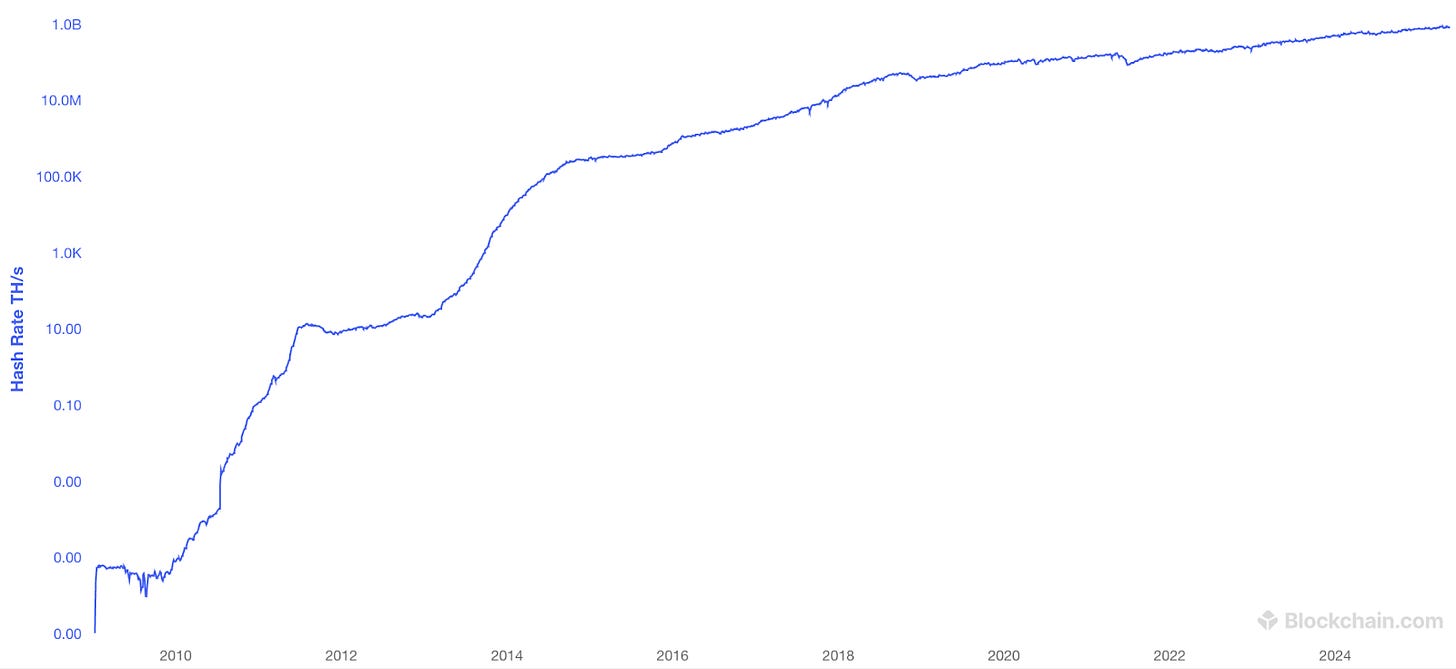
I mentioned earlier that today, about 6 x 1023 hashes are needed to mine a Bitcoin block. This wasn’t always the case! In earlier eras, there was much less compute power running on the Bitcoin network, as shown by this (log-scale) chart:
The number of hashes needed to mine a block was therefore previously much lower, and has been changing continuously over time. The way this change is implemented is through the “difficulty-adjustment mechanism”. Essentially, every 2016 blocks, the network looks at the timestamps of blocks on the chain to estimate what the current hashrate is, and readjusts the difficulty so that blocks keep coming every ten minutes on average.
An important thing to note, though, is that there are relatively loose restrictions on the timestamps. As long as timestamps aren’t doing something crazy like moving backwards in time or taking hours between blocks, the difficulty adjustment mechanism will just accept them. This is therefore a potential avenue for attack.
Longest Chain vs. Strongest Chain
This leads us to a discussion of the true meaning of the “longest chain rule”. In my opinion, this term is somewhat misleading, because it suggests that the block considered to be the tip of the chain is the one with the most blocks below it. Technically, this is not how the chain tip is decided. If it were, it would open the possibility for an attacking chain to be built by setting timestamps to cause a low total difficulty and mining a ton of blocks that way.
Bitcoin might be better described as a “strongest chain” blockchain: The consensus chain tip is the one with the most total work below it. This prevents a classical attacker from using the difficulty adjustment mechanism to their advantage, because no matter what difficulty they set the chain to, they still only have <49% of the hash power, so the total work on their chain cannot grow faster, on average and in the limit, than the main chain.
Attack via Difficulty Increase
Unfortunately, this leads to a confluence of factors that make it possible for a quantum miner to attack! Grover’s algorithm provides a quadratic relationship between the amount of iterations performed and the probability of success. So if the difficulty is quadrupled, the Grover miner only takes twice as long to mine a block as it otherwise would, and so the rate at which the miner adds work to the chain doubles. In principle, the miner can just keep on doubling the difficulty until it is adding work faster than the rest of the network.
What does all this mean for Bitcoin in the long-term?
There are some solid counterarguments to the vision of Bitcoin’s future presented in this post, which I would now be remiss not to point out.
The “Conditions for Advantageous Quantum Bitcoin Mining” work assumes a fully-fault tolerant quantum computer, which likely already puts the time frame of the risk on the order of decades, rather than years. A fully-fault-tolerant quantum computer would also be necessary to run Shor’s algorithm - if the authors of the articles I linked above were only focusing on Shor because they knew the risks from it would come first, then that’s fair. I still feel that the risks from Grover are somehow more fundamental. One can, in principle, use Bitcoin as it exists today but with post-quantum signatures to avoid the risks from Shor’s algorithm, but it is hard for me to imagine a non-controversial change to Bitcoin that entirely avoids the risks from Grover’s algorithm. This is primarily because any such change would likely mean making pre-existing mining hardware (which is optimized very specifically for the task of mining bitcoin as it is today) much less effective, and therefore worth much less to their current owners.
But it’s true that the computational requirements of the attacks I’ve described are even more extreme than those of a Shor attack. For the centralization-related risks to be realized, the quantum computer would not only need to be fault-tolerant, but would also need to be sufficiently cheap to run and build and would need a sufficiently high clock speed to be within, if not a few, at least a handful of orders of magnitude of classical computers.
While there is some debate on whether it will ever be possible to build fault-tolerant quantum computers, I think most computer scientists and physicists come down against complete impossibility. Notwithstanding this, perhaps it is reasonable to think that, for reasons of materials science, it might never be possible to build logical quantum computers that function at clock speeds within an order of magnitude of classical computers. The question becomes: How fast can quantum computers really be made, and will it be fast enough to Grover mine? In my mind, the answer is far from certain. Many sources today emphasize that error correction consumes a large amount of compute, but perhaps once quantum computing becomes viable, more effort will be put in to more reliable engineering and stronger refrigeration techniques to cut down on the necessity of lots of error correction. In the interest of open debate, I’m making a Manifold market on the fastest rate of Grover iterations for Bitcoin hash computation that will be experimentally demonstrated by 2060.
The time-warp attack doesn’t have the same requirement on speed. But it does, obviously, get slower the slower the quantum computer that runs it. We concluded that it would require a number of 2-week epochs roughly proportional to the inverse of the square of the proportion of blocks obtained by the miner running at the honest difficulty to the rest of the network. Even a miner that was able to produce blocks at 10% of the speed of the honest network would take at least 4 years to complete their attack, and if they were only able to produce blocks at 1% of the speed, the attack would take centuries.
So there is some doubt that these failure modes will ever manifest. Nevertheless, I think their hypothetical existence casts some doubt on the robustness of Nakamoto consensus and the idea that Bitcoin is destined to be a civilizational currency.
On some level, I think calling this an "algorithm" is misleading, you can imagine situations (as we shall see) where you would want to "turn the crank" for a while, pause to check if you want to open the register immediately, turn the crank some more, and only then open the output. Perhaps this is a source of confusion.
Interestingly, you can also “turn the crank backwards”, but that won’t be relevant for today’s post.
Alternatively, by applying k = 0.583 · √N iterations, we could get an 84% chance of successfully solving the problem. You might notice that this actually solves, in expectation, about 13% more problems per unit time than the 0.785 way. Yet explanations of Grover’s algorithm always seem to focus on the way that gets closest to 100% chance of solution the first time you measure.
“Cost” consisting of the cost of energy and the amortized cost of development and production of the hardware.
Not necessarily a good assumption, see the end of the post for more disclaimers.
The median of an exponential distribution is ln(2) ≈ 0.69 times the mean, so the median Bitcoin block time is about 7 minutes.
Note also: The optimization that leads to the 15.936 minutes number assumes that no sibling blocks will be accepted. If the miner optimizes for sibling blocks, even more will be produced.
Technically, the above analysis assumes they don’t and there is some interesting game theory about how quantum miners should time their blocks to not get scooped, see Lee et al. “Strategies for quantum races”, and the analysis below.
See Carlsten et al. “On the Instability of Bitcoin Without the Block Reward” for a definition of this term.